ASC_8384 的个人博客

论文心得双栏，最后一页保持平衡使用 pbalance

- 阅读全文 -

炼丹心得清空显存sudo fuser -v /dev/nvidia* |awk '{for(i=1;i<=NF;i++)print "kill -9 " $i;}' | sudo sh或者查找fuser -v /dev/nvidia*https://zhuanlan.zhihu.com/p/637164912nvitopnvidia-ml-py is conflict w

- 阅读全文 -

论文阅读计划2023-09[x] BAI J, BAI S, CHU Y, 等, 2023. Qwen Technical Report[M/OL]. arXiv[2023-10-05]. http://arxiv.org/abs/2309.16609.[x] BEURER-KELLNER L, FISCHER M, VECHEV M, 2023. Prompting Is Programming

- 阅读全文 -

All in OnePVEwebgui 白屏F12 可以看到 501 no such file '/PVE/StdWorkspace.js'。方案：apt install --reinstall proxmox-widget-toolkit apt update && apt upgrade apt install -f apt dist-upgrade pvecm updat

- 阅读全文 -

StableDiffusionAttributeError: module 'modules.shared' has no attribute 'artist_db'在升级后报错，删掉roll-artist即可。Anyone know why I get this error and how I can fix it?Additional Networks Lora 模型在extensions\s

- 阅读全文 -

PyCharmpydevd AttributeError: module '_pydevd_bundle_ext.pydevd_cython' has no attribute 'trace_dispatch'在调试代码的时候，遇到以下报错：AttributeError: module '_pydevd_bundle_ext.pydevd_cython' has no attribute 'tra

- 阅读全文 -

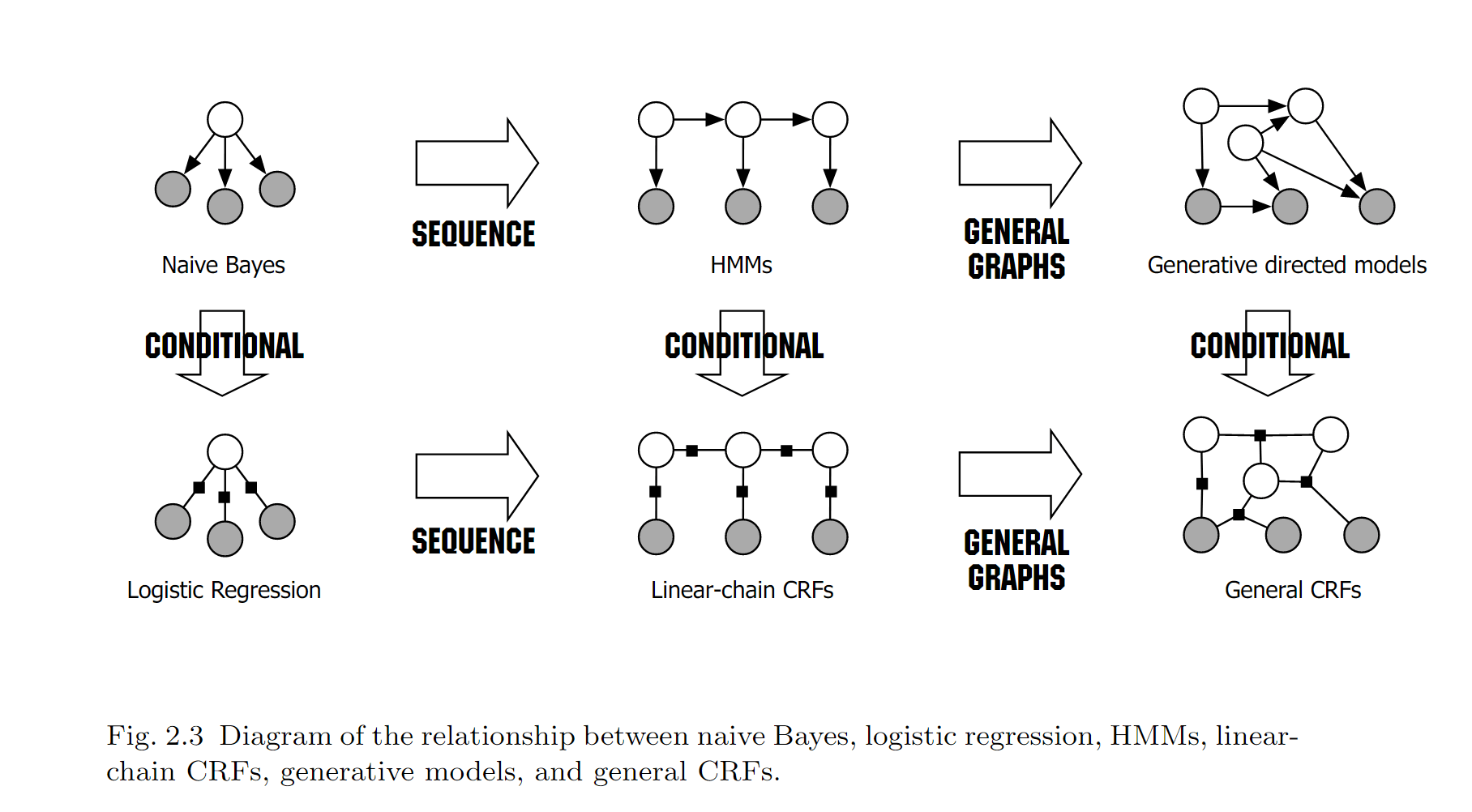
CRFtag: #NLP #Basis条件随机场（conditional random field，简称 CRF），是一种鉴别式机率模型，是随机场的一种，常用于标注或分析序列资料，如自然语言文字或是生物序列。先来张《自然语言处理入门》的图。可以浅显地认为，机器学习就是给你随机变量 $x$，求（预测）出另一些随机变量 $y$。如果 $y$ 是连续型随机变量（如明天的股价），那就是回归问题；如果是离散

- 阅读全文 -

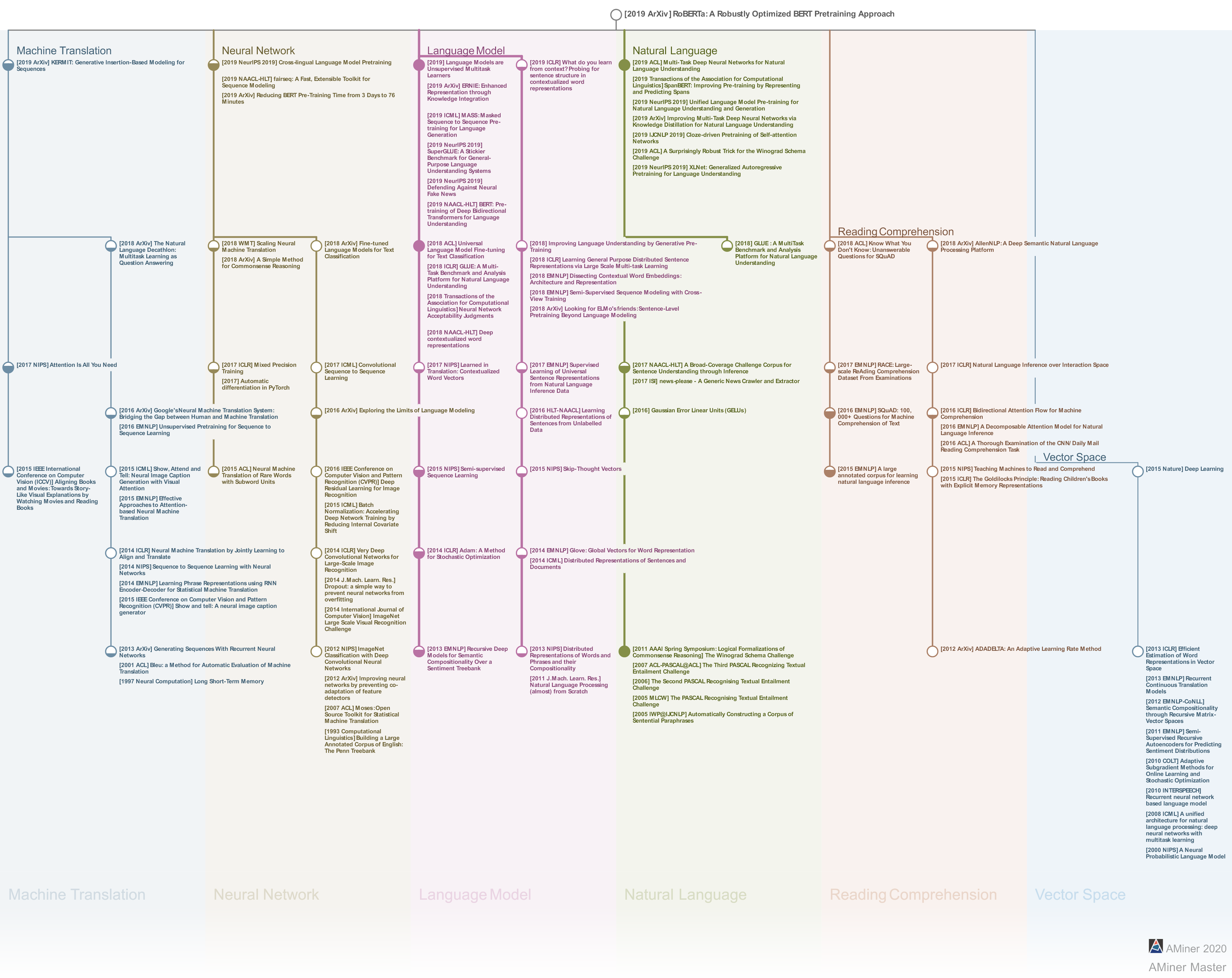
RoBERTa: A Robustly Optimized BERT Pretraining Approachtag: #ReadPaper #NLPQ1 论文试图解决什么问题？如何使用更好的超参数与数据集对 BERT 进行充分的训练。Q2 这是否是一个新的问题？学疏才浅，不清楚，但应该是的。不谈 novelty， 自从 BERT 提出后，在其框架上做出一些改动获得一些效果，这种想法应该是显而易见

- 阅读全文 -

NERWikipediaNamed-entity recognition (NER) (also known as (named) entity identification, entity chunking, and entity extraction) is a subtask of information extraction that seeks to locate and classif

- 阅读全文 -